Ориентирование карты: Ориентирование на местности по карте
Свежие карты спортивного ориентирования. Страница 1 из 518
16 декабря 2022 г.
Новогодние старты
Район: спринт
Дистанция: 5.90 km
25 сентября 2022 г.
Марафон на Холмах Яппиля 2022
Страна: Россия
Район: Зеркальное
Дисциплина: лонг
Дистанция: 12.78 km
15 октября 2022 г.
Красный Лист 2022 спринт 2 круг
Страна: Россия
Район: р-н Промышленный
Дисциплина: спринт
Дистанция: 2.42 km
15 октября 2022 г.
Красный Лист 2022 спринт 1 круг
Страна: Россия
Район: р-н Промышленный
Дисциплина: спринт
Дистанция: 3.79 km
4 ноября 2022 г.
Алоль Осенняя 2022 спринт
Страна: Россия
Район: турбаза Алоль
Дисциплина: кросс-спринт
Дистанция: 4.33 km
9 июля 2022 г.
Иван Купала 2022 (2 день)
Страна: Россия
Район: оз. Белое
Дисциплина: средняя
Дистанция: 6.52 km
12 июля 2022 г.
Рельеф и Гидрография 2022
Страна: Россия
Район: оз.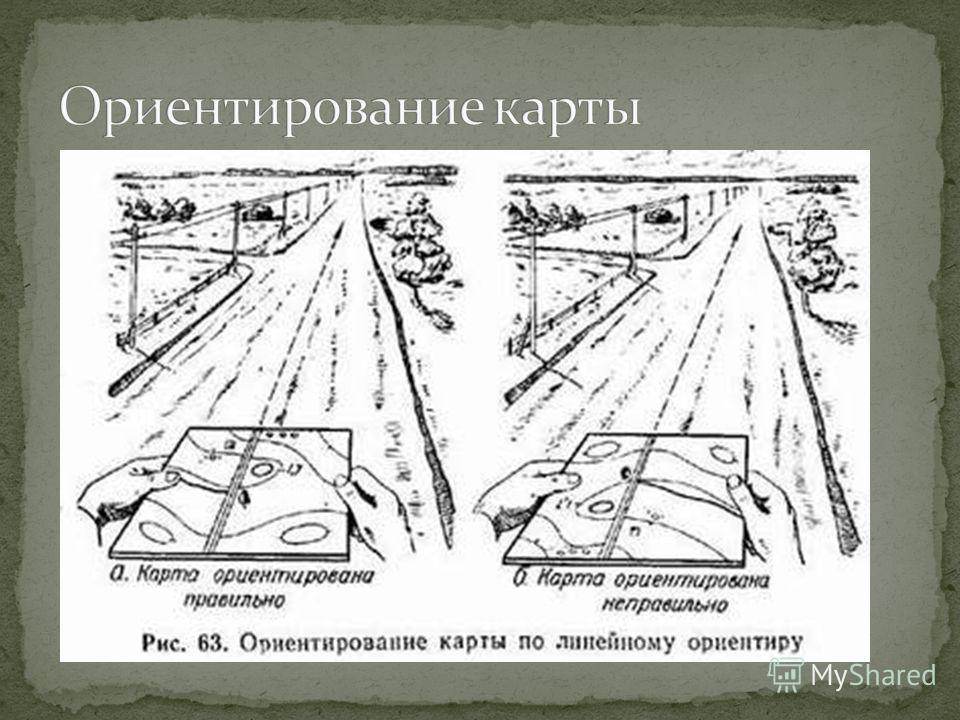 Белое
Белое
Дисциплина: классика
Дистанция: 7.68 km
6 декабря 2022 г.
Тренировочный старт
Дистанция: 2.73 km
3 декабря 2022 г.
Тренировочный старт
Дистанция: 6.94 km
7 августа 2022 г.
Фестиваль активного отдыха 2022
Страна: Россия
Район: оз. Долгое
Дисциплина: выбор
Дистанция: 7.14 km
1.5. Ориентирование карты.
Наверное, самый простой из них — это использование компаса. Нужно положить компас на карту, и развернуть карту так, чтобы северная стрелка расположилась параллельно северным линиям карты. Обратите внимание на то, чтобы не перепутать севери юг.
Обратите внимание на то, чтобы не перепутать севери юг.
А как же поступить, если компаса у вас нет? Существует еще один способ. Для его использования необходимо знать свою точку стояния на карте. Отыщите на местности какой-нибудь ориентир, найдите его и на карте. Затем поворачивайте карту до тех пор, пока воображаемые линии, проведенные из точки вашегостояния к этому ориентиру, не совпадут на картеи местности. Если же вы стоите на дороге, разверните карту так, чтобы эта дорога на карте стала параллельна этой же дороге на местности.
Умея ориентировать карту по местным предметам, можно определить направление на озеро (см. параграф1.3.), без использования компаса. Сориентировав карту по расположению дороги и домика лесника, продолжим линию, соединяющую нашу точку стояния и озеро. Эталиния и будет искомым направлением. Теперь главное —не потерять этого направления при движении в густом бору.
Как, двигаясь без компаса по лесу, можно сохранить прямолинейность движения? В солнечный день можно запомнить угол между тенью и направлением движения. Акак быть в пасмурныйдень?
Акак быть в пасмурныйдень?
Школьникам, изучающим геометрию, известна аксиома: «Через две точки можно провести прямую, причем только одну». Именно эта аксиома лежит в основе предлагаемого способа.
Посмотрев в направлении требуемого движения, заметим на некотором расстоянии какой-нибудь приметный ориентир — дерево, куст и т. п. Затем, смотря далее в этом же направлении, заметим еще один ориентир, лежащий на одной прямой с первым и с точкой нашего стояния. Будем двигаться вперед до первого ориентира.Дойдя до него, посмотрим через второй ориентир вперед и выберем следующий, третий ориентир. Затем дойдем до второго ориентира и так далее.
Выбор впереди себя объекта, к которому нужно двигаться — самый точный и надежный способ движения по азимуту.
Но, двигаясь по лесу, нам постоянно приходится обходить различные препятствия: деревья, муравейники, завалы. Чтобы не сойти с азимута, нужно обходить такие препятствияпоочередно то слева, то справа, то есть «змейкой».
А чтобы не сбиться при обходе большого препятствия, например озера, нужно в направлении азимутазасечь на противоположном берегу ориентир. Обойти озеро, дойти до этого ориентираипродолжить от него движение по азимуту.
Обойти озеро, дойти до этого ориентираипродолжить от него движение по азимуту.
Задания для самостоятельной работы.
- На поляне или во дворе расставлено 8–12 КП. На каждом КП лежит «карта» с расположением всех КП. Нужно сориентировать карту по окружающим КП.
- Двигаясь с одного КП на другой, нарисовать на листе бумаги расположение видимых КП относительно отрезка вашего движения.
- КП расставлены на открытой площадке. На каждом КП — карточка, на которой изображенперегон с этого КП на следующий и северные линии. Сориентировав карточку по компасу, определить, какой пункт брать следующим. Пройти весь маршрут.
- Аналогично предыдущему заданию. Но на карточках нет северных линий, зато указаны номера КП. Сориентировав карточку по КП, нанести на нее северные линии.
- Выполнить те же задания в парке (лесу) на реальной карте. По мере роста уверенности соседний КП можно ставить за пределами видимости.
- Написал Алексей Абрамов kontur.
 tk
tk
- ВКонтакте
Download SocComments v1.3
| < Предыдущая | Следующая > |
|---|
Compare-Contrast-Connect: Map Orientation and Shape
NGSS Science and Engineering Practices:
NGSS Crosscutting Concepts:
Представление информации в таблице, диаграмме или карте может быть столь же или даже более важным, чем слова, сопровождающие его. Например, люди часто помнят изображение из учебника по естествознанию задолго до того, как забыли слова, написанные рядом с изображением, объясняющие его. Хотя ориентация или форма карты могут показаться безобидными, они могут оказать существенное влияние на восприятие относительной важности различных мест.
Ориентация карты. Верх — это новый низ
На большинстве карт Земли север находится вверху (поэтому север находится вверху). Однако эта ориентация карты произвольна. Помещение севера вверху карты стало стандартным, когда европейские исследования были на пике в 16 веке. Возможно, это произошло потому, что европейцы использовали для навигации Полярную звезду и магнитные компасы, а может быть, просто потому, что им нравилось держаться на вершине мира. Несмотря на это, ориентация карты с севером вверху привела к тому, что люди стали называть места «выше» или «ниже» других. Люди также говорят, что они путешествуют «вверх» или «вниз», чтобы посетить эти места. Поскольку люди часто предполагают, что рост коррелирует с важностью, соглашение о севере вверху укрепляет идею о том, что страны или люди на севере более важны, чем на юге. Когда Южный полюс повернут так, что он находится «вверху» на карте, незнакомая ориентация заставляет людей смотреть на мир с новой точки зрения (SF рис. 1.6).
Однако эта ориентация карты произвольна. Помещение севера вверху карты стало стандартным, когда европейские исследования были на пике в 16 веке. Возможно, это произошло потому, что европейцы использовали для навигации Полярную звезду и магнитные компасы, а может быть, просто потому, что им нравилось держаться на вершине мира. Несмотря на это, ориентация карты с севером вверху привела к тому, что люди стали называть места «выше» или «ниже» других. Люди также говорят, что они путешествуют «вверх» или «вниз», чтобы посетить эти места. Поскольку люди часто предполагают, что рост коррелирует с важностью, соглашение о севере вверху укрепляет идею о том, что страны или люди на севере более важны, чем на юге. Когда Южный полюс повернут так, что он находится «вверху» на карте, незнакомая ориентация заставляет людей смотреть на мир с новой точки зрения (SF рис. 1.6).
Форма карты — карты Меркатора
Карты в проекции Меркатора — это тип карты с цилиндрической проекцией, обычно используемый в классах. В то время как все карты каким-то образом искажают земную поверхность, проекция Меркатора отображает сильно искаженное изображение площади и границ суши. Это связано с тем, что карта Меркатора отображает сферическую Землю в виде прямоугольника с перпендикулярными линиями долготы и широты, тогда как на самом деле эти линии круглые. Карты Меркатора полезны для морской навигации, но они не годятся для изучения Земли. Карта Меркатора вызвала много путаницы в отношении географии (SF рис. 1.7 A) по сравнению с другими типами картографических проекций (например, псевдоцилиндрическими картами, SF рис. 1.7 B). Например, на карте Меркатора Европа выглядит больше, чем Южная Америка, а Африка выглядит такого же размера, как Гренландия. В действительности Южная Америка более чем на 50% больше Европы, а Гренландия — в четырнадцать раз меньше Африки.
В то время как все карты каким-то образом искажают земную поверхность, проекция Меркатора отображает сильно искаженное изображение площади и границ суши. Это связано с тем, что карта Меркатора отображает сферическую Землю в виде прямоугольника с перпендикулярными линиями долготы и широты, тогда как на самом деле эти линии круглые. Карты Меркатора полезны для морской навигации, но они не годятся для изучения Земли. Карта Меркатора вызвала много путаницы в отношении географии (SF рис. 1.7 A) по сравнению с другими типами картографических проекций (например, псевдоцилиндрическими картами, SF рис. 1.7 B). Например, на карте Меркатора Европа выглядит больше, чем Южная Америка, а Африка выглядит такого же размера, как Гренландия. В действительности Южная Америка более чем на 50% больше Европы, а Гренландия — в четырнадцать раз меньше Африки.
Карты передают данные, но они также передают идеи и мнения. При просмотре карты помните, что каждый тип обеспечивает уникальную перспективу, и важно понимать эту перспективу, чтобы правильно использовать и интерпретировать карту.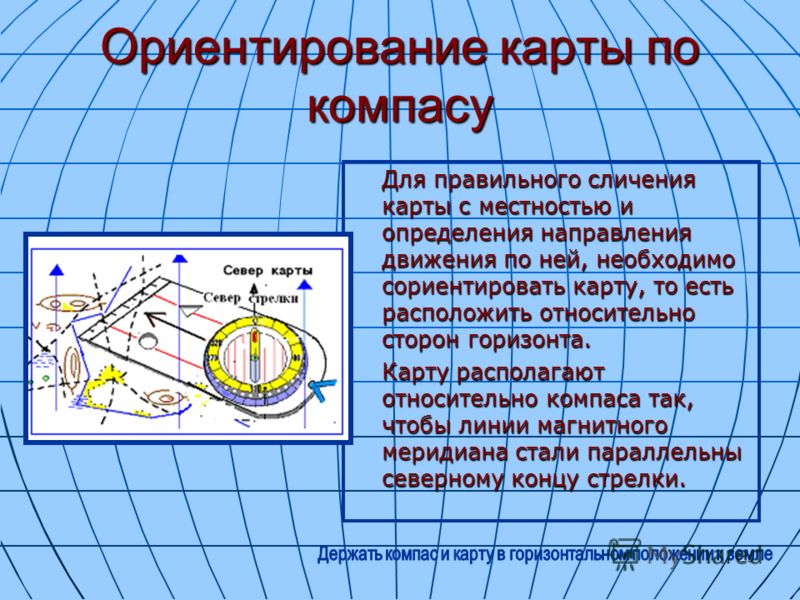
Набор вопросов:
- «Перевернутая» карта проекции Меркатора ясно показывает, как континенты сгруппированы в северном полушарии, и делает Южную Америку особенно заметной. Какие еще наблюдения о Земле вы можете сделать с этой точки зрения, которые вы, возможно, не заметили на обычной карте?
- При сравнении проекции Меркатора с псевдоцилиндрической картой или с глобусом, какие области искажаются больше всего? Какие области наименее искажены? Есть ли что-то общее в расположении наиболее и наименее искаженных областей?
- Карты Меркатора могут быть сосредоточены на любом регионе мира, от бассейна Тихого океана до Ближнего Востока. Как вы думаете, почему картографы предпочитают центрировать карты в разных регионах? Узнайте, используют ли в разных странах преимущественно карты, сосредоточенные на разных областях, и если да, то почему.
Различные проекции карты влияют на наше восприятие мира. Это видно в звездообразных и сердцевидных картографических проекциях на SF Рис.
 1.8. Эти картографические проекции были разработаны, чтобы подчеркнуть особенности планеты Земля. Используйте SF рис. 1.8, чтобы ответить на вопросы с 4 по 7.
1.8. Эти картографические проекции были разработаны, чтобы подчеркнуть особенности планеты Земля. Используйте SF рис. 1.8, чтобы ответить на вопросы с 4 по 7.
- Звездообразная проекция карты (SF рис. 1.8 A) была разработана таким образом, что Северный полюс, область, часто искаженная на других картографических проекциях, находится в центре карты, что делает ее наименее искаженной областью. Южное полушарие было разделено на доли (концы звезды) и развернуто вокруг неповрежденного северного полушария, чтобы оба полушария были видны. Как проекция звездной карты влияет на ваше восприятие мира?
- Псевдоконическая картографическая проекция в форме сердца (SF рис. 1.8 B) была разработана в 1500-х годах и широко использовалась для карт мира и некоторых континентальных карт в 17 веке. Преимущество карты в форме сердца заключается в том, что центр карты имеет небольшое искажение, и, хотя искажение увеличивается по направлению к полюсам, видны все континенты северного полушария, а карта сохраняет цилиндрическую форму Земли.
 Как проекция карты в форме сердца влияет на ваше восприятие мира?
Как проекция карты в форме сердца влияет на ваше восприятие мира?
- Изучите историю других картографических проекций и то, как они влияют на восприятие мира зрителем.
Тип специального элемента:
Содержание:
3.2: Ориентация и масштаб карты
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5469
- Deline, Harris & Tefend
- Университет Западной Джорджии через GALILEO Open Learning Materials
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Делайн, Харрис и Тефенд
- Лицензия
- СС BY-SA
- Программа OER или Publisher
- ГАЛИЛЕО
- Показать оглавление
- нет
- Теги

7
7
Все топографические карты, подготовленные Геологической службой США (USGS), ориентированы севером вверху карты. Поэтому, если вы определяете позицию на карте и движетесь к верхней части карты, вы движетесь в северном направлении, а если вы двигаетесь к нижней части карты, вы движетесь к югу.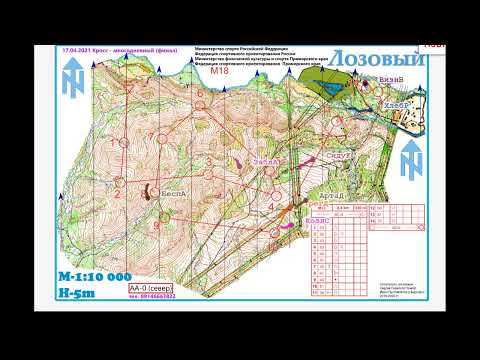 Любое движение вправо будет направлено на восток, а движение влево будет направлено на запад. Стороны этих карт ориентированы параллельно линиям долготы, которые представляют собой воображаемые линии, огибающие земной шар и ориентированные так, что они проходят через северный и южный географические полюса. Начиная с линии долготы 0° (известной как нулевой меридиан), которая проходит через город Гринвич, Англия, эти линии увеличиваются до 180° в обоих направлениях к востоку и западу от нулевого меридиана (рис. 3.1). Это может помочь визуализировать линии долготы, если вы думаете об апельсине, который, если его очистить, покажет части апельсина, ориентированные как линии долготы, которые делят Землю. Все линии долготы сходятся в центре апельсина (или географических северном и южном полюсах Земли).
Любое движение вправо будет направлено на восток, а движение влево будет направлено на запад. Стороны этих карт ориентированы параллельно линиям долготы, которые представляют собой воображаемые линии, огибающие земной шар и ориентированные так, что они проходят через северный и южный географические полюса. Начиная с линии долготы 0° (известной как нулевой меридиан), которая проходит через город Гринвич, Англия, эти линии увеличиваются до 180° в обоих направлениях к востоку и западу от нулевого меридиана (рис. 3.1). Это может помочь визуализировать линии долготы, если вы думаете об апельсине, который, если его очистить, покажет части апельсина, ориентированные как линии долготы, которые делят Землю. Все линии долготы сходятся в центре апельсина (или географических северном и южном полюсах Земли).
Верхний и нижний края топографической карты ориентированы так, что они параллельны линиям широты , которые являются воображаемыми линиями, огибающими земной шар и ориентированными под прямым углом к оси Земли. Линия широты 0° — это экватор Земли ; линии широты увеличиваются до 90 ° северной широты или 90 ° южной широты от экватора, так что северный полюс имеет широту 90 ° северной широты, а южный полюс имеет широту 90 ° южной широты.
Линия широты 0° — это экватор Земли ; линии широты увеличиваются до 90 ° северной широты или 90 ° южной широты от экватора, так что северный полюс имеет широту 90 ° северной широты, а южный полюс имеет широту 90 ° южной широты.
Эта система координат широты и долготы позволяет однозначно определить положение на Земле при условии, что значения широты всегда определяются их положением на севере или юге от экватора, а долгота определяется как восток или запад от экватора. нулевой меридиан. Градус широты или долготы представляет собой большое расстояние на Земле, поэтому градусы далее подразделяются на минуты (минута расстояния — это не то же самое, что минута времени!), а эти минуты расстояния далее подразделяются на секунды. В 1° широты или долготы 60 минут (60 футов) расстояния, а в одной минуте 60 секунд (60 дюймов) расстояния. Примером точного местоположения на поверхности Земли может быть 33°34’22» северной широты, 85°05’46» западной долготы (местоположение автора на момент написания этой главы!), что читается как «33 градуса, 34 градуса».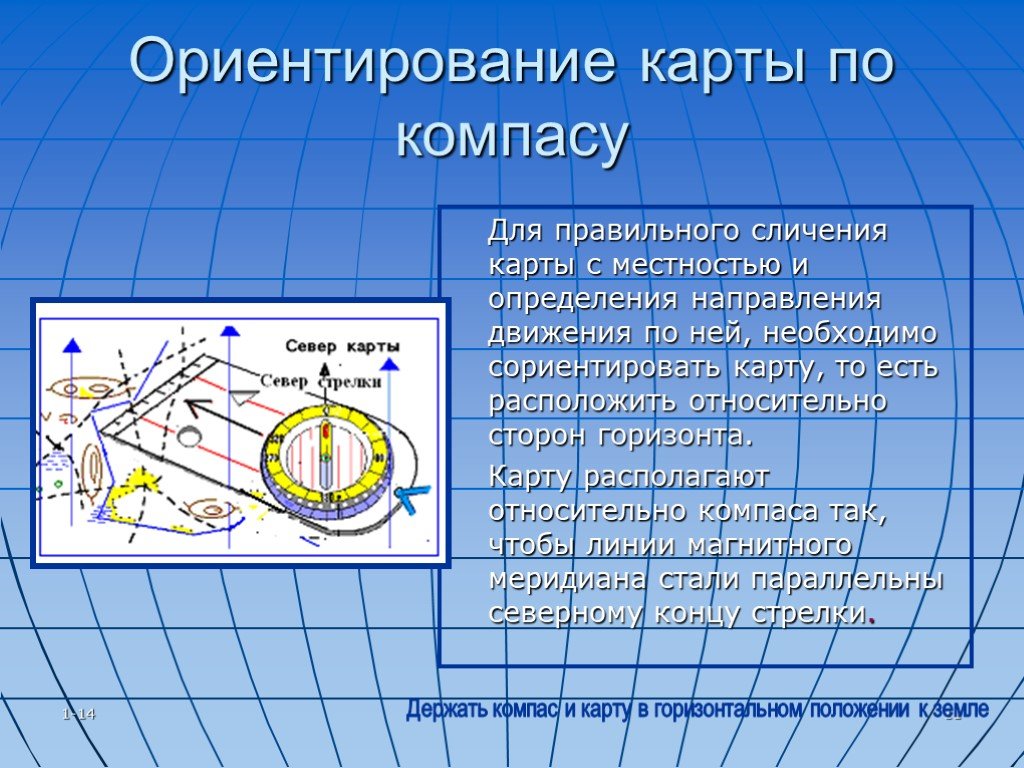 минуты 22 секунды северной широты и 85 градусов 5 минут 46 секунд западной долготы».
минуты 22 секунды северной широты и 85 градусов 5 минут 46 секунд западной долготы».
Координаты широты и долготы каждой топографической карты находятся в углах карты. Часто эти карты представляют собой область Земли, расстояние до которой меньше одного градуса. Например, обычная топографическая карта покажет только 7,5 минут расстояния (7 футов 30 дюймов) как по широте, так и по долготе; в этом случае верхний и нижний края карты будут представлять расстояние в 7,5 минут по широте, а левый и правый края карты будут представлять расстояние в 7,5 минут по долготе. Поскольку степень расстояния на карте неизменна, в определенных местах на краю карты отображается сокращенное обозначение изменения минут и секунд. Только в углах карты будут включены градусы для координат широты и долготы. См. приведенный выше пример, на котором показан правый верхний угол 7,5-минутной карты или 7,5-минутного четырехугольника (форма большинства топографических карт). Дополнительные числа, кроме широты и долготы, также показаны по краям карты; это другая система сетки, и здесь она не будет объясняться.
Помните, что верхний и нижний края топографической карты ориентированы параллельно линиям широты. На рис. 3.2 верхний край карты представляет собой линию широты. Таким образом, координаты, которые меняются при перемещении по верхней части карты (в направлении восток-запад), должны быть координатами долготы, поскольку широта не должна меняться. Нижний край этой карты не показан но вы можете предсказать, какой должна быть широта по нижнему краю: это карта региона в Аризоне и, поскольку Аризона расположена к северу от экватора, линии широты должны увеличиваться от нижней части карту к верхней части карты (поскольку все линии широты увеличиваются по мере продвижения к северу от экватора). Для 7,5-минутной карты увеличение широты от нижнего угла к верхнему углу должно составлять ровно 0°7’30” северной широты. Это дает нижнему углу карты широту 36°00’00” северной широты.0007
Все карты представляют собой уменьшенную версию изображаемого ими региона мира; если бы это было не так, то карта, которую человек должен иметь при себе, была бы точно такого же размера, как город (если это карта города) или размер штата (если это карта штата). Представьте, что вы пытаетесь носить с собой карту всей страны! Слово «масштаб» относится к степени уменьшения, и все карты имеют масштаб карты, чтобы указать, насколько площадь на карте была уменьшена. Масштаб карты предусмотрен для того, чтобы читатель карты мог точно определить, какое расстояние фактически представлено на его карте, или измерить расстояние между двумя точками на карте, или даже рассчитать уклон холма или реки. Двумя широко используемыми масштабами карты на топографической карте являются линейная шкала (или графическая шкала) и дробная шкала (также известная как шкала отношений).
Представьте, что вы пытаетесь носить с собой карту всей страны! Слово «масштаб» относится к степени уменьшения, и все карты имеют масштаб карты, чтобы указать, насколько площадь на карте была уменьшена. Масштаб карты предусмотрен для того, чтобы читатель карты мог точно определить, какое расстояние фактически представлено на его карте, или измерить расстояние между двумя точками на карте, или даже рассчитать уклон холма или реки. Двумя широко используемыми масштабами карты на топографической карте являются линейная шкала (или графическая шкала) и дробная шкала (также известная как шкала отношений).
На рис. 3.3 представлены три шкалы; каждая полоса представляет собой графическое представление расстояния на карте, и читатель карты должен решить, хотят ли они измерять расстояния в километрах, метрах, милях или футах. Чтобы найти расстояние между любыми двумя точками на карте, человек может использовать лист бумаги, чтобы перенести две точки на линейчатую шкалу и считать расстояние непосредственно с линейчатой шкалы. Обратите внимание, что каждая линейка шкалы имеет начальную точку (ноль) внутри шкалы, а не в конце каждой шкалы (рис. 3.3).
Обратите внимание, что каждая линейка шкалы имеет начальную точку (ноль) внутри шкалы, а не в конце каждой шкалы (рис. 3.3).
Другим типом масштаба карты является дробный масштаб; на рис. 3.3 дробный масштаб равен 1:24 000. Никакие единицы не сообщаются, поскольку это соотношение 1 к 24 000 действительно для любой единицы измерения при условии, что это одна и та же единица. Например, если используются дюймы, то этот масштаб карты указывает, что 1 дюйм на карте фактически покрывает 24 000 дюймов земли (расстояние между двумя точками в реальном мире). Или, если использовать сантиметры, то 1 сантиметр на карте фактически покрывает 24 000 сантиметров земли. Если бы наша карта была того же размера, что и область, которую она представляет (например, карта комнаты, в которой вы сейчас сидите), то дробный масштаб вашей карты был бы 1:1, а ваша карта была бы точно такого же размера, как ваша комната! Это снова возвращает нас к определению карты, которая представляет собой уменьшенную версию региона, для представления которого она предназначена; карты, которые сильно уменьшены (сильно уменьшены), называются картами мелкого масштаба, даже если они представляют большие участки Земли.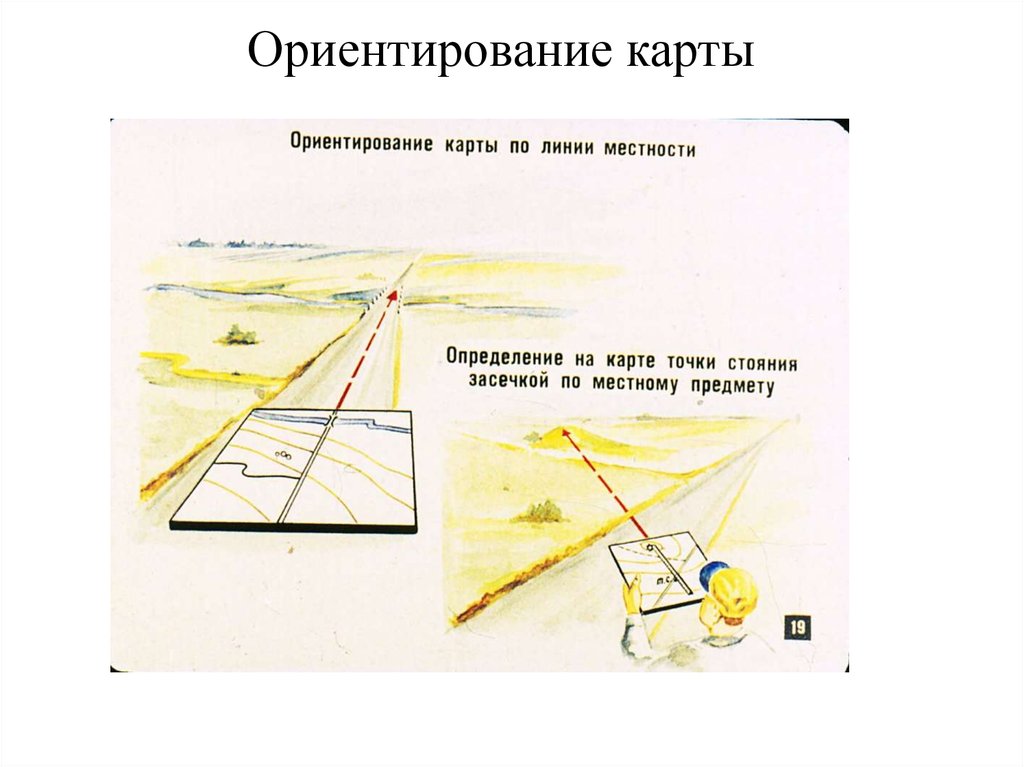 Например, карта масштаба 1:500 000 покажет большую часть Земли, но мелкие детали будут потеряны (например, расположение зданий или улочек), тогда как карта масштаба 1:12 000 является крупномасштабной картой, хотя на ней изображена гораздо меньшая часть. области поверхности Земли, но видны детали (например, здания, дороги и другие ориентиры). Поместив кончик пальца на поверхность мелкомасштабной карты, можно охватить территорию в несколько миль, а на крупномасштабную карту (например, 1:12 000) можно охватить только \(\frac{1}{10}\) мили.
Например, карта масштаба 1:500 000 покажет большую часть Земли, но мелкие детали будут потеряны (например, расположение зданий или улочек), тогда как карта масштаба 1:12 000 является крупномасштабной картой, хотя на ней изображена гораздо меньшая часть. области поверхности Земли, но видны детали (например, здания, дороги и другие ориентиры). Поместив кончик пальца на поверхность мелкомасштабной карты, можно охватить территорию в несколько миль, а на крупномасштабную карту (например, 1:12 000) можно охватить только \(\frac{1}{10}\) мили.
Одно из преимуществ использования дробной или относительной шкалы заключается в том, что можно использовать любую единицу измерения, а при необходимости легко выполнять преобразования. Например, для карты масштаба 1:12 000 1 дюйм на карте равен 12 000 дюймов на поверхности Земли, а поскольку в 1 футе 12 дюймов, мы также можем сказать, что 1 дюйм на карте равен 1000 футам на поверхности Земли. поверхности Земли (переведите 12 000 дюймов в футы, умножив на коэффициент преобразования \(\frac{1\;ft}{12\;in}\)).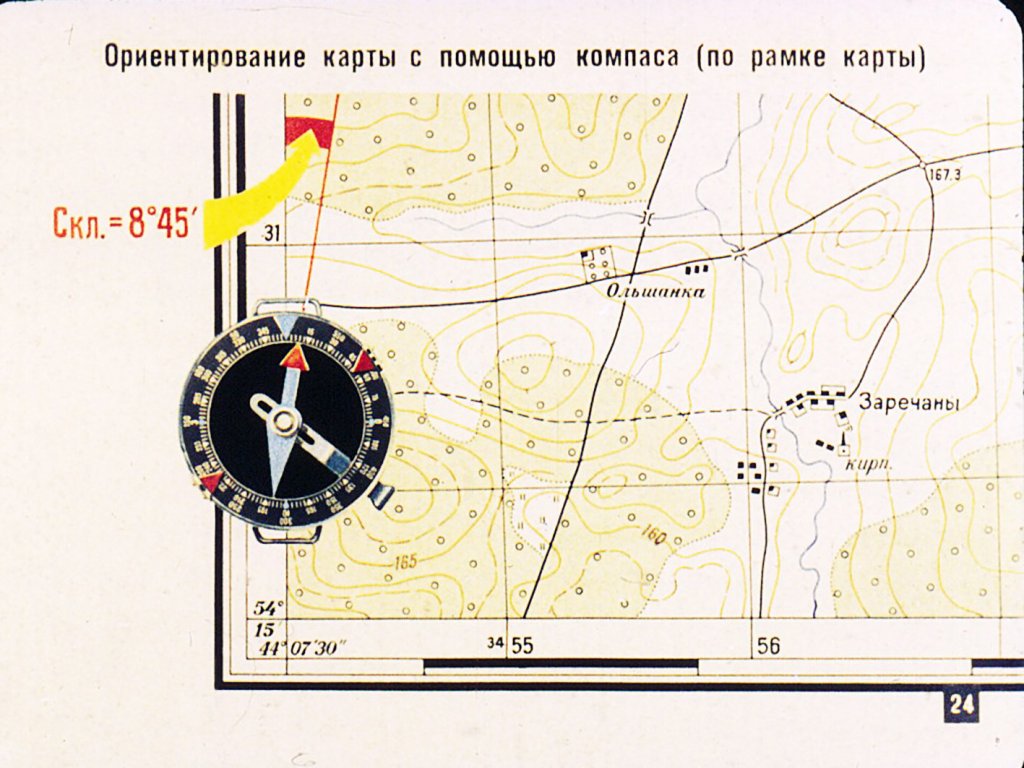 Простая вербализация этого масштаба с помощью фразы «на этой карте 1 дюйм соответствует 1000 футам» — это третий тип масштаба карты, который по очевидным причинам называется словесным масштабом. Написание фразы «1 дюйм равен 1000 футам» — это способ добавить словесный масштаб к вашей карте.
Простая вербализация этого масштаба с помощью фразы «на этой карте 1 дюйм соответствует 1000 футам» — это третий тип масштаба карты, который по очевидным причинам называется словесным масштабом. Написание фразы «1 дюйм равен 1000 футам» — это способ добавить словесный масштаб к вашей карте.
| Таблица 3.1: Некоторые полезные коэффициенты преобразования | |
| 1 фут = 12 дюймов | 1 метр = 3,28 фута |
| 1 миля = 5280 футов | 1 миля = 63 360 дюймов |
| 1 километр = 1000 метров | 1 километр = 0,62 мили |
Помните, что, поскольку коэффициенты преобразования равны, например, 1 фут = 12 дюймов, то деление одного на другое (\(\frac{1\;ft}{12\;in}\)) дает 1, а поскольку умножение чего-либо на 1 не меняет никакого значения, все, что мы на самом деле делаем, — это меняем единицы измерения.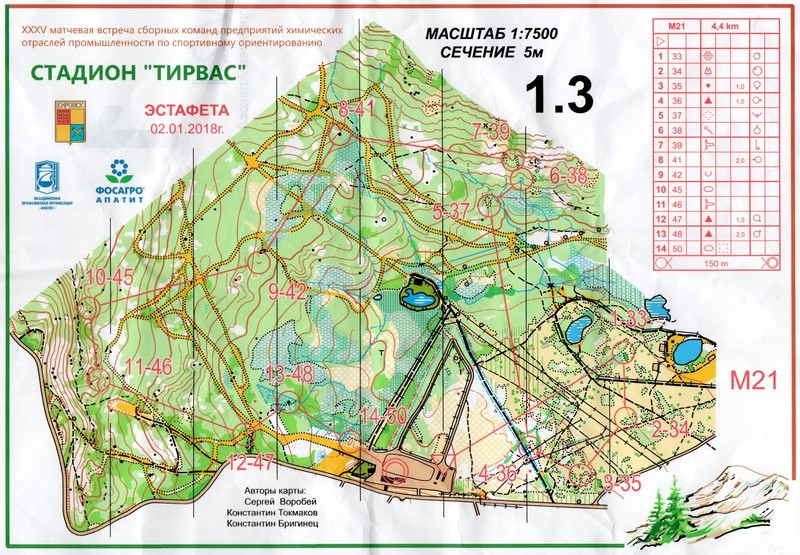 Следовательно, вычисление 5,5 футов x (\(\frac{12\;in}{1\;фут}\)) позволит выразить 5,5 футов в дюймах, что в данном случае будет равно 66 дюймам.
Следовательно, вычисление 5,5 футов x (\(\frac{12\;in}{1\;фут}\)) позволит выразить 5,5 футов в дюймах, что в данном случае будет равно 66 дюймам.
Эта страница под названием 3.2: Ориентация и масштаб карты распространяется по лицензии CC BY-SA, автором, ремиком и/или куратором которой являются Deline, Harris & Tefend (GALILEO Open Learning Materials).

 tk
tk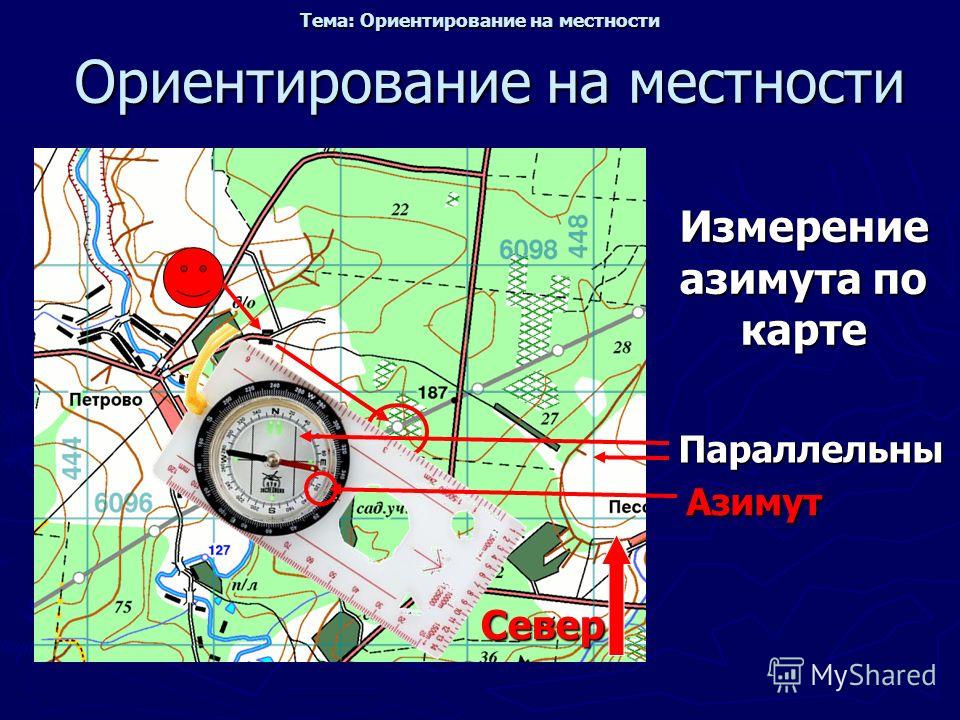 1.8. Эти картографические проекции были разработаны, чтобы подчеркнуть особенности планеты Земля. Используйте SF рис. 1.8, чтобы ответить на вопросы с 4 по 7.
1.8. Эти картографические проекции были разработаны, чтобы подчеркнуть особенности планеты Земля. Используйте SF рис. 1.8, чтобы ответить на вопросы с 4 по 7. Как проекция карты в форме сердца влияет на ваше восприятие мира?
Как проекция карты в форме сердца влияет на ваше восприятие мира? 