Линии условно проведенные по поверхности земли параллельно экватору: что такое меридиан, а что такое паралель
Градусная сетка — География — справочник
| Градусная сетка |
ГРАДУСНАЯ СЕТКА Порой людям в их хозяйственной деятельности или в исследованиях очень важно определить точное местонахождение каких-либо географических объектов на поверхности Земли. Это можно сделать с помощью градусной сетки, которая есть на каждой карте или глобусе. Она состоит из линий параллелей и меридианов. Земля вращается вокруг своей оси. Это воображаемая линия. Места выхода этой воображаемой линии на поверхность Земли называются полюсами. У Земли есть Южный и Северный полюс. Кратчайшая линия, условно проведенная на глобусе от одного полюса к другому, называется меридианом. В переводе на русский язык слово «меридиан» означает «полуденная линия». Действительно, ее направление совпадает с направлением тени от предметов в полдень. Если идти все время по направлению этой тени, то можно обязательно прийти к Северному полюсу, а если в обратную сторону — то к Южному. Часть окружности называют дугой. Величину дуги измеряют градусами. Полуокружность, в данном случае меридиан, содержит 180°. Зная это, можно подсчитать длину 1°. Она равна 111 км на любом участке меридиана. Параллели — линии, условно проведенные по поверхности Земли параллельно экватору. Экватор — условно проведенная линия, находящаяся на равном расстоянии от Северного и Южного полюсов. Экватор — это самая длинная параллель. Ее длина 40 000 км. Длина параллелей уменьшается к полюсам. Самая короткая параллель — полюс. Она обозначается точкой. Параллели имеют форму окружности. Длина 1° на экваторе, так же как и на меридиане, составляет 111 км. По направлению к полюсам длина 1° уменьшается. Параллель тоже можно провести из любой точки. С помощью градусной сетки на глобусе и карте можно определить стороны горизонта, а также точное местоположение какого-либо объекта по его географическим координатам. Изображение меридианов и параллелей на глобусе и физической карте полушарий различно. На глобусе все меридианы — полуокружности, а параллели — окружности. На карте полушарий экватор и средний меридиан изображены прямыми линиями, а все остальные меридианы и параллели — кривыми линиями разной длины. Такое искажение возникает вследствие изображения выпуклой поверхности на плоскости. При этом искажаются не только линии градусной сетки, но и очертания объектов, их площади. Наименьшие искажения возникают у экватора, наибольшие — у полюсов.
|
Назад
Презентация для урока географии в 5 классе «Параллели и меридианы.
 Градусная сеть»
Градусная сеть»
Скрыть поздравление
Посмотреть все поздравления
Смирнова Марина Юрьевна
С Новым годом! С новым счастьем всех! Главное, чтобы был мир на земле, чтобы дети вернулись к родителям живыми и здоровыми! Всем желаю мира, согласия!
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи▪Презентации
Материал опубликовала
#5 класс #География #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование
Параллели и меридианы.
Градусная сеть.
АВТОР: Кушнарёва Т.Н.
Градусная сеть — это система меридианов и параллелей на картах и глобусах для определения географических координат.
Это интересно!!!
Параллели и меридианы были нанесены еще на первые географические карты. Так до наших дней сохранились карты Дикеарха Мессианского (3 век до н.э.), на которые были нанесены параллели. Первые географические сетки не имели градусных различий: параллели и меридианы изображались в виде прямых линий.
Первые карты
Меридиан — линия, которая проходит от северного полюса к южному [красная линия на рисунке]
Нулевой меридиан(Гринвичский), это меридиан, от которого начитается отсчёт долготы.
Меридиан???
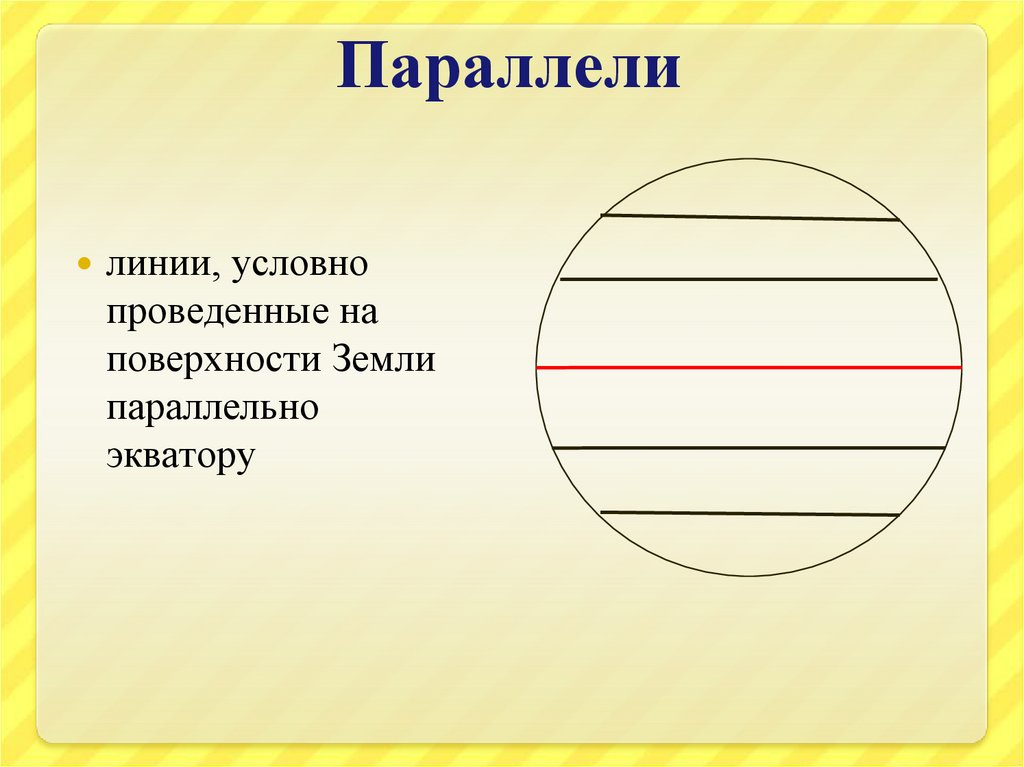
Параллели – это линии, условно проведенные на поверхности земли параллельно экватору.
Параллели — линии, параллельные экватору, направлены с запада на восток.
Параллели???
ЭТО ИНТЕРЕСНО!!!
ВИДЕО РОЛИК
Задание:
1. Покажите на карте параллель 0°, как она называется?
2. Какие параллели па карте пересекают Африку?
Какие параллели па карте пересекают Африку?
3. Какая параллель на карте ближе всего расположена к Северному полюсу?
Задание:
1.Покажите на карте меридиан 0°, как он называется?
2. Какие меридианы на карте пересекают Евразию?
3. Какие меридианы на карте в Западном полушарии, а какие в Восточном? Почему?
Задание: В каком полушарии (Западном или Восточном) расположены следующие географические объекты: г. Москва и г. Ростов-на-Дону; материк Южная Америка; о. Мадагаскар.
Задание: В каком полушарии (Северном или Южном) расположены следующие географические объекты: государство Россия; материк Австралия; о.Гренландия.
стр.1
стр.1
|
Это утверждение неверно — TOK RESOURCE.ORG
Одна из версий парадокса лжеца, впервые описанная Зеноном Элейским [495-430 г. до н.э.]
ЗАНЯТИЕ ДЛЯ КЛАССА I: ПАРАДОКС ЛЖЕЦА
Некоторые логические головоломки, подобные этой версии парадокса лжеца, подрывают общепринятые представления об абсолютной достоверности и абсолютной непротиворечивости в здании чистой математики.
После того, как первоначальный дискомфорт, вызванный этим умопомрачительным парадоксом, исчезнет, и учащиеся сами увидят, что это непростая логическая головоломка, последует оживленный обмен мнениями.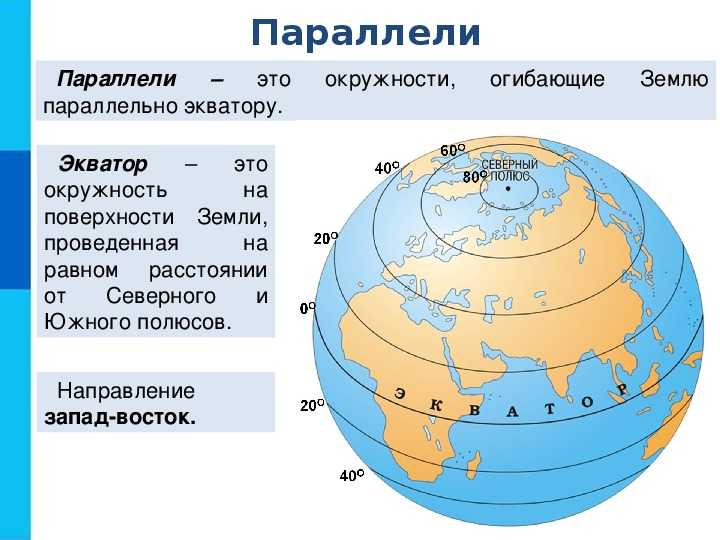 Следующие наводящие вопросы могут добавить или не добавить ценности.
Следующие наводящие вопросы могут добавить или не добавить ценности.
Итак, утверждение истинно или ложно?
Это самореферентное утверждение? Что такое самореферентность и почему она здесь проблематична?
Мы обычно связываем аналитические области чистой математики и логики с уверенностью. В какой степени существование случайных парадоксальных результатов подрывает предположение об определенности?
ПАРАДОКС ЦИКРОВАРЯ
Старое фото парикмахерской Frantz, Анахайм, Калифорния.
Продолжите беседу с классом: Если парикмахеры — это те, кто бреет мужчин тогда и только тогда, когда они не бреются сами, то бреются ли парикмахеры? Спросите учащихся, что они думают? Конечно, вскоре возникает противоречие; но просто сказать, что рассматриваемый парикмахер должен быть женщиной, которая не бреется, или сказать, что предложение просто не имеет смысла, являются проницательными ответами, но они просто выпрыгивают из рассмотрения парадокса.
Сообщите учащимся, что в начале 20-го века известные математики (включая Рассела, Уайтхеда, Фреге и Гильберта) стремились создать прочную основу для всей математики, основанную на логической достоверности. Парадоксы подорвали их возвышающиеся амбиции, и в 1930 году такие благородные, но, в конечном счете, высокомерные попытки были навсегда покончены со знаменитой теоремой Гёделя о неполноте.
Следующие цитаты очень показательны, и учащимся следует помнить о них при выполнении письменного задания «Платоники против формалистов», которое следует за этим разделом.
«Я хотел определенности, как люди хотят религиозной веры. Я думал, что в математике можно найти больше уверенности, чем где-либо еще. Но я обнаружил, что многие математические доказательства, которые мои учителя ожидали от меня, были полны заблуждений, и что если в математике действительно можно обнаружить достоверность, то она должна быть в новой области математики с более прочным основанием, чем те, которые были раньше.
до сих пор считалось безопасным. Но по ходу работы мне постоянно вспоминалась басня о слоне и черепахе. сконструировав слона, на котором мог бы покоиться математический мир, я обнаружил, что слон шатается, и приступил к конструированию черепахи, чтобы слон не упал. Но черепаха была не более надежна, чем слон, и после примерно двадцати лет очень тяжелого труда я пришел к выводу, что больше ничего не могу сделать для того, чтобы сделать математическое знание несомненным.
— Бертран Рассел в «Портретах по памяти и других очерках» (1956)
«Цель моей теории — раз и навсегда установить достоверность математических методов… Нынешнее положение дел, когда мы сталкиваемся с парадоксами, невыносимо. Подумать только, определения и дедуктивные методы, которым все учатся, учат и пользуются в математике, образце доказательства и достоверности, ведут к абсурду! Если математическое мышление ущербно, то где нам найти истину и достоверность? Д
— Дэвид Гильберт: О бесконечности (1926)
Эйнштейн и Гёдель во время одной из своих обычных прогулок в Принстоне, штат Нью-Джерси.
ЗАДАНИЕ ДЛЯ КЛАССА II: НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Напомните учащимся, что вся евклидова геометрия построена на пяти самоочевидных аксиомах и постулатах. Спустя столетия стало очевидно, что доказать пятый постулат Евклида (постулат о параллелях) проблематично. Признание того, что постулат параллелей не был столь самоочевидным, как остальные четыре постулата, привело к открытию неевклидовой геометрии, в которой постулат параллелей считается ложным.
Гиперболические неевклидовы поверхности выпуклы и имеют седловидную форму. Параллельные прямые сходятся. Эллиптические неевклидовы поверхности вогнуты. Параллельные прямые расходятся. Знакомый пример — поверхность сферы.
Чем отличается сумма углов треугольника в неевклидовой геометрии.
РУКИ НА ЗАДАЧЕ С НАСТОЯЩИМ ГЛОБУСОМ
Для этого практического занятия учащиеся должны работать втроем. Заранее до начала занятий позаботьтесь о том, чтобы под рукой были школьные глобусы, линейки, веревки, ленты и транспортиры.
Заранее до начала занятий позаботьтесь о том, чтобы под рукой были школьные глобусы, линейки, веревки, ленты и транспортиры.
1. Проведите учащихся через следующий мысленный эксперимент:
Сначала убедитесь, что вы знаете разницу между линиями широты и линиями долготы. Самая известная линия широты – это экватор. Все остальные линии широты параллельны экватору и уменьшаются по мере приближения к полюсам. Все линии долготы представляют собой «большие круги», подобные экватору, и проходят через Северный и Южный полюса. Линии долготы условно отстоят друг от друга на 15 градусов. Почему?
Джеэкспло / Wikimedia Commons
Представьте себе линию долготы, пересекающуюся с экватором. Какова величина образовавшегося угла? Теперь мысленно переместитесь по экватору туда, где следующая линия долготы пересекается с экватором. Опять же, какова величина угла, образованного между ними? Далее представьте себе равнобедренный треугольник с основанием, являющимся частью экватора между двумя линиями долготы, отстоящими друг от друга на пятнадцать градусов.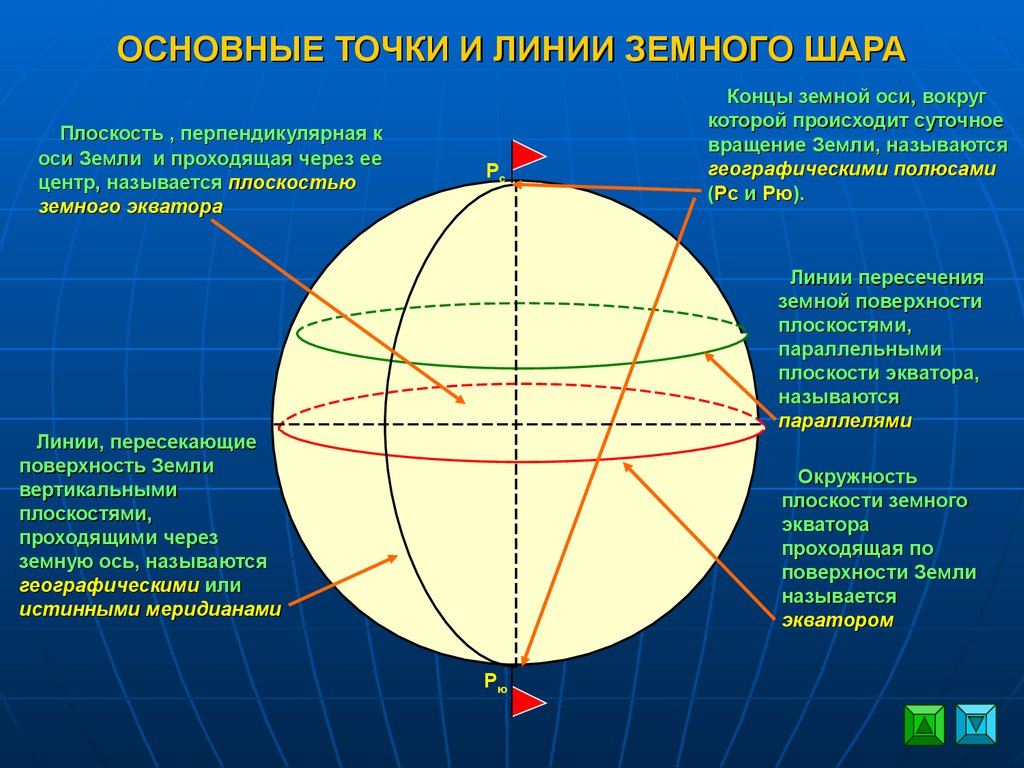 Стороны треугольника — это в точности две линии долготы, которые сходятся по мере удаления от основания, в конечном итоге пересекаясь на северном полюсе, образуя угол в 15 градусов. Чему равна сумма углов треугольника?
Стороны треугольника — это в точности две линии долготы, которые сходятся по мере удаления от основания, в конечном итоге пересекаясь на северном полюсе, образуя угол в 15 градусов. Чему равна сумма углов треугольника?
2. На глобусе отметьте 3 случайных креста на трех разных континентах (чтобы расстояние между ними было значительным). Используйте натянутую нить и ленту, чтобы определить треугольник, образованный соединением точек. С помощью транспортира тщательно измерьте сумму углов треугольника.
3. Сначала выберите свой любимый европейский город. Затем определите два разных маршрута полета между Сан-Франциско и выбранным пунктом назначения на основе карты Google выше 9.0012
A. Прямо с запада на восток.
B. Двигаясь с востока на запад, но по пути сворачивая на север, вы проходите через арктическую Канаду, Гренландию и Исландию.
Используйте эластичную нить и ленту, чтобы отметить два пути.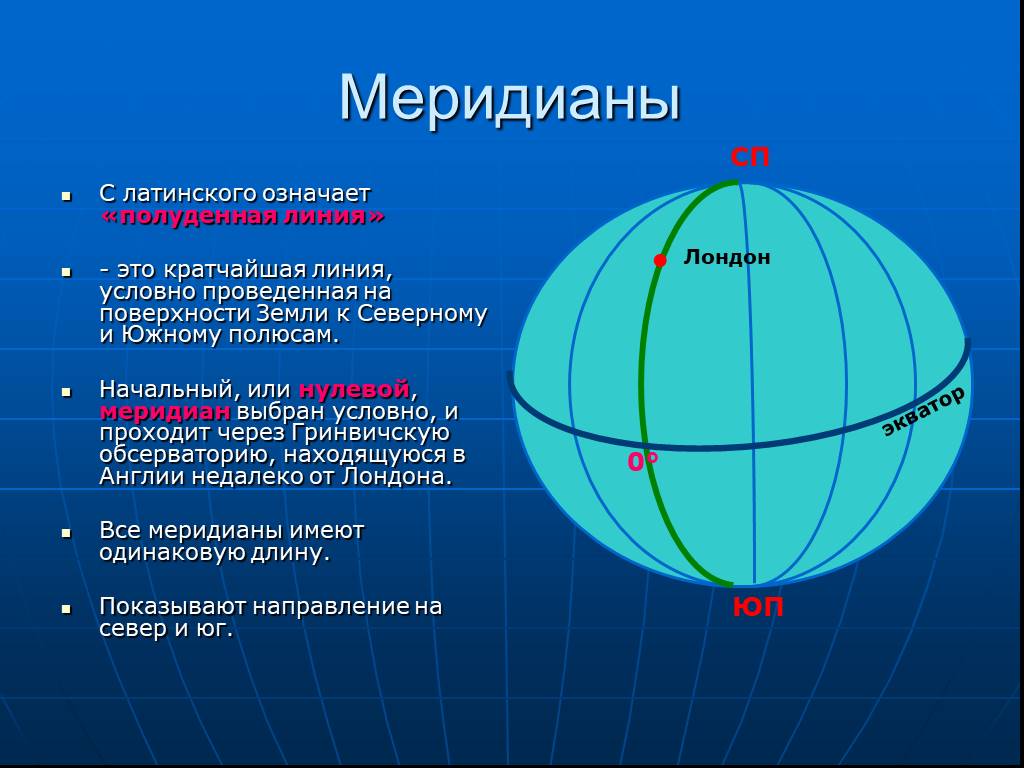

 Меридиан можно провести через любую точку на поверхности Земли, и в каждой точке он будет направлен на север и на юг. Все меридианы на глобусе или на карте представляют собой полуокружности. Они все имеют одинаковую длину.
Меридиан можно провести через любую точку на поверхности Земли, и в каждой точке он будет направлен на север и на юг. Все меридианы на глобусе или на карте представляют собой полуокружности. Они все имеют одинаковую длину. Так как параллель направлена с запада на восток, то она будет перпендикулярна меридиану. В полдень по тени можно определить линию меридиана и параллели в данной точке.
Так как параллель направлена с запада на восток, то она будет перпендикулярна меридиану. В полдень по тени можно определить линию меридиана и параллели в данной точке. Из этого определения два условия
Из этого определения два условия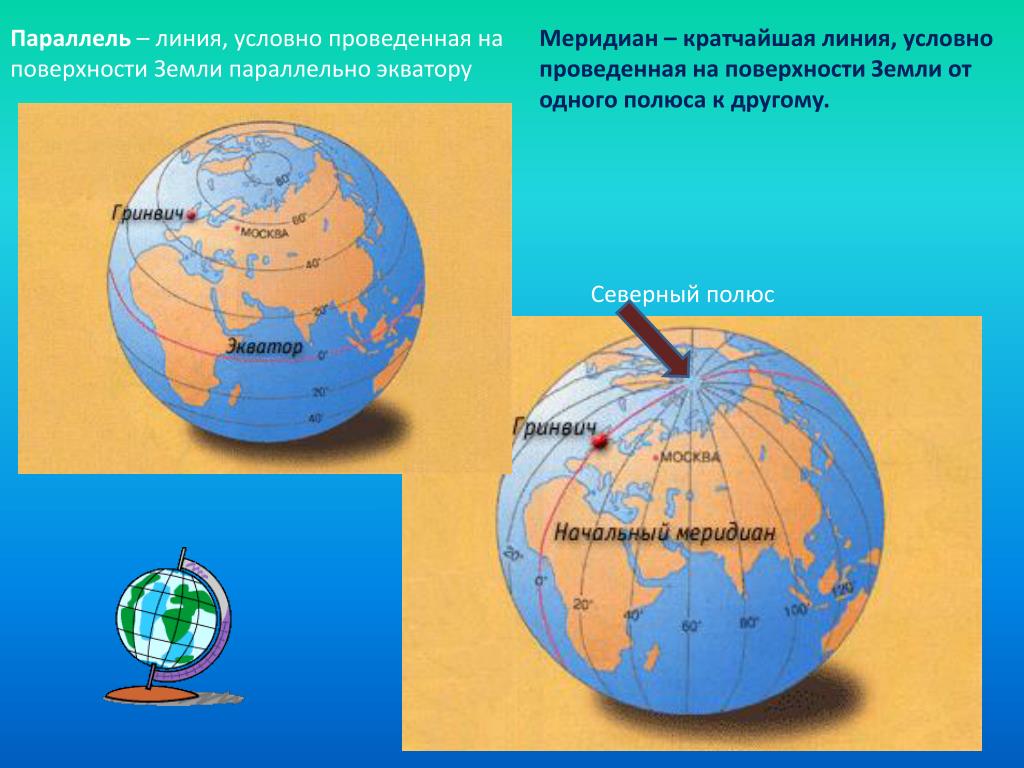 Такие плоскости параллельны экватору и
Такие плоскости параллельны экватору и Эта плоская плоскость лежит вдоль
Эта плоская плоскость лежит вдоль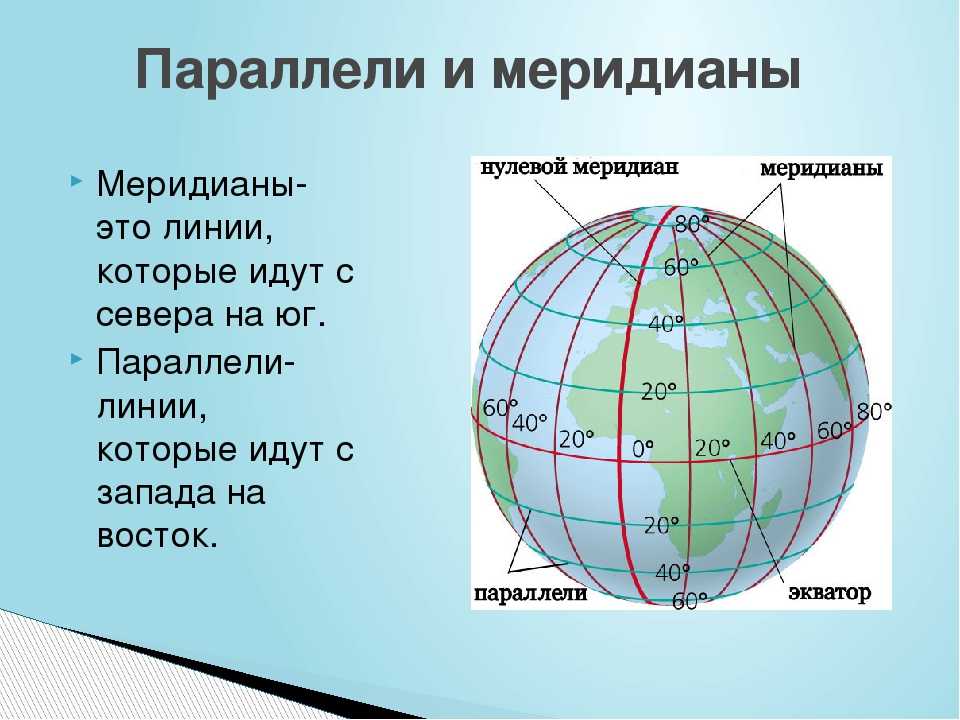 Таким образом, имея равный радиус
Таким образом, имея равный радиус
 Это движение создает легкий вздутие
Это движение создает легкий вздутие
 до сих пор считалось безопасным. Но по ходу работы мне постоянно вспоминалась басня о слоне и черепахе. сконструировав слона, на котором мог бы покоиться математический мир, я обнаружил, что слон шатается, и приступил к конструированию черепахи, чтобы слон не упал. Но черепаха была не более надежна, чем слон, и после примерно двадцати лет очень тяжелого труда я пришел к выводу, что больше ничего не могу сделать для того, чтобы сделать математическое знание несомненным.
до сих пор считалось безопасным. Но по ходу работы мне постоянно вспоминалась басня о слоне и черепахе. сконструировав слона, на котором мог бы покоиться математический мир, я обнаружил, что слон шатается, и приступил к конструированию черепахи, чтобы слон не упал. Но черепаха была не более надежна, чем слон, и после примерно двадцати лет очень тяжелого труда я пришел к выводу, что больше ничего не могу сделать для того, чтобы сделать математическое знание несомненным.